Matematická abstrakce systému zettelkasten
V článku Implementujeme digitální zettelkasten (1. část): laboratorní rozbor jsem v sekci Luhmannův unikátní způsob propojování poznámek neformálně popsala, jak Luhmann v systému zettelkasten propojoval své permanentní poznámky. Konkrétně jsem zmínila takzvané implicitní a křížové propojení. Na intuitivní úrovni tyto pojmy snad dávají smysl, ale má vnitřní teoretická informatička je toužila definovat přesněji. A proto vznikl tento článek.
V tomhle článku se na zettelkasten podíváme z abstraktního matematického pohledu. Podíváme se na něj jako na datovou strukturu. Nebojte, nemusíte mít žádné předchozí znalosti z teoretické informatiky, vystačíte si jen s chutí a zájmem o toto téma. Vše vysvětlím. Všechny potřebné pojmy zadefinuji a ukážu na příkladech. A pokud teorii grafů již ovládáte, můžete klidně následující vysvětlení přeskočit a podívat se rovnou na sekci Matematická abstrakce 🤯 systému zettelkasten.
Připraveni? Přenechávám tedy už plně slovo teoretičce Elišce. Děj se vůle její!
Nelineární struktura 🕸 zvaná graf
Ehm (teoretička Eliška si odkašlává), děkuji za předání slova. Tak tedy. Luhmannův zettelkasten je ukázkou takzvané nelineární datové struktury. Datové struktury slouží k ukládání dat (Well, duh.) a patří mezi základní výbavu každého informatika. Rozdělit je můžeme právě na lineární a nelineární. Tyhle struktury ale nepotkávají v každodenním životě jen informatici. Potkáváme je my všichni. Například silniční síť, propojení přátel na sociální síti nebo internet jsou příklady nelineární datové struktury, kterou v informatice nazýváme graf.
Pod pojmem graf si ale nepředstavujte grafy koláčové nebo sloupcové, které se používají v manažerských prezentacích. Nemyslím tím ani grafické znázornění průběhu funkce, které nás učili zakreslovat ve školách při hodinách matematiky. Grafem zde budeme rozumět základní objekt z teorie grafů.
Graf definujeme jako uspořádanou dvojici množiny vrcholů a množiny hran. Vrcholy reprezentují atomické objekty, ve kterých jsou uložena data, a hrany reprezentují vztah mezi dvěma vrcholy (objekty). V kontextu silniční sítě by vrcholy reprezentovaly města a hrany propojení dvou měst silnicí. V případě sociální sítě, například Facebooku, bychom za vrcholy považovali jednotlivé profily lidí a hrana mezi dvěma vrcholy by vyjadřovala, že odpovídající dva lidé jsou přátelé.
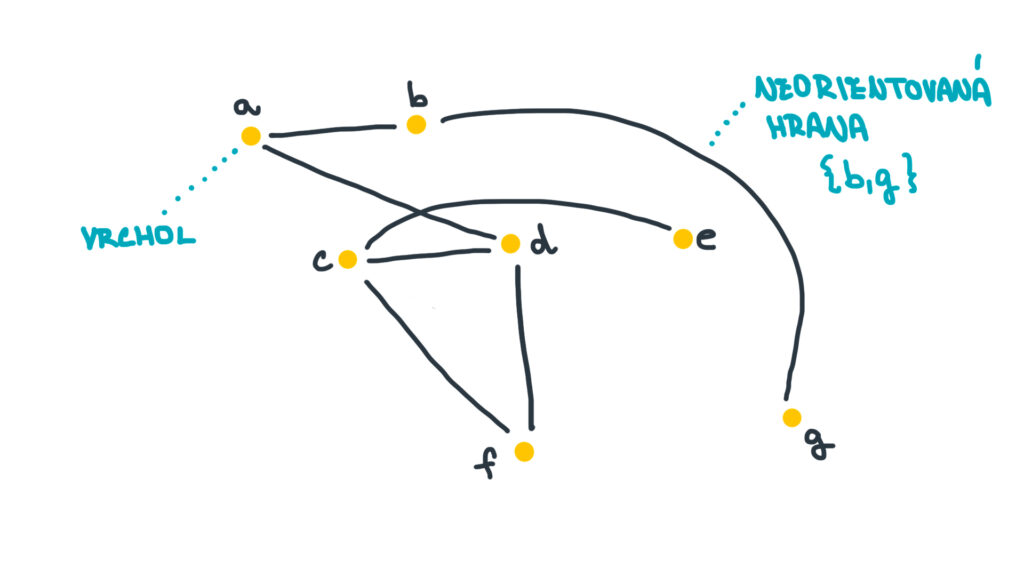
Graf můžeme zakreslit obrázkem — vrcholy značíme kolečkem a hranu spojující dva vrcholy zakreslíme jako čáru (úsečku) mezi nimi. Takovým hranám se přesněji říká neorientované hrany a matematicky je zapisujeme jako neuspořádanou dvojici (množinu) dvou vrcholů. Vrcholy propojené neorientovanou hranou jsou v takovém vztahu rovnocennými partnery (v teorii grafů je nazýváme sousedními vrcholy). Graf, který používá pouze neorientované hrany, nazýváme neorientovaným grafem.
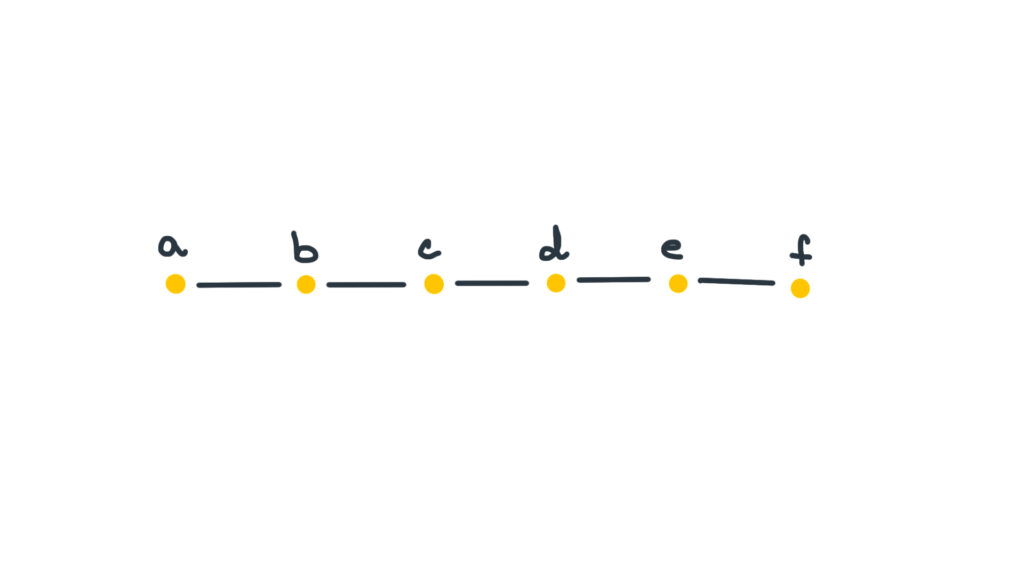
Na obrázku 1 je obrázkově zakreslený příklad neorientovaného grafu, který má 7 vrcholů a 7 hran. Matematicky bychom tento graf zapsali následovně: \(G_1 = (V_1, E_1)\), kde
- \(V_1 = \big\{ a, b, c, d, e, f, g \big\}\) a
- \(E_1 = \big\{ \{a,b\}, \{b,g\}, \{a,d\}, \{c,d\}, \{c,e\}, \{c,f\}, \{d,f\} \big\}\).
Tedy máme graf pojmenovaný \(G_1\), který se skládá z množiny vrcholů \(V_1\) a množiny hran \(E_1\). Například vrcholy \(a\) a \(b\) jsou v tomto grafu sousedními vrcholy (sousedy), protože jsou propojeny hranou. Vrcholy \(a\) a \(c\) ale sousedé nejsou, protože mezi nimi hrana nevede.
Hádáte správně, že kromě neorientovaných hran, můžeme mít i hrany orientované. Ty matematicky zapisujeme jako uspořádané dvojice vrcholů a v obrázku je zakreslujeme jako šipky. Pokud máme hranu vedoucí z vrcholu \(u\) do vrcholu \(v\), tj. hranu \((u,v)\), pak vrchol \(u\) nazýváme předchůdcem vrcholu \(v\) a vrchol \(v\) následníkem vrcholu \(u\). Graf, který používá pouze orientované hrany, nazýváme orientovaným grafem.
Příkladem orientovaného grafu v reálném životě je třeba Twitter a vztah sledování — zde by profily byly vrcholy a pokud sledujete například můj profil, tak by vedla z vašeho vrcholu orientovaná hrana do mého vrcholu. Já vás ale sledovat zpět nemusím (tough love, sorry), proto je hrana orientovaná. Pokud bych vás ale nazpět sledovala, pak by do grafu přibyla další orientovaná hrana. Jedna by tedy vedla od vás ke mně a druhá ode mě k vám. Dává to smysl?
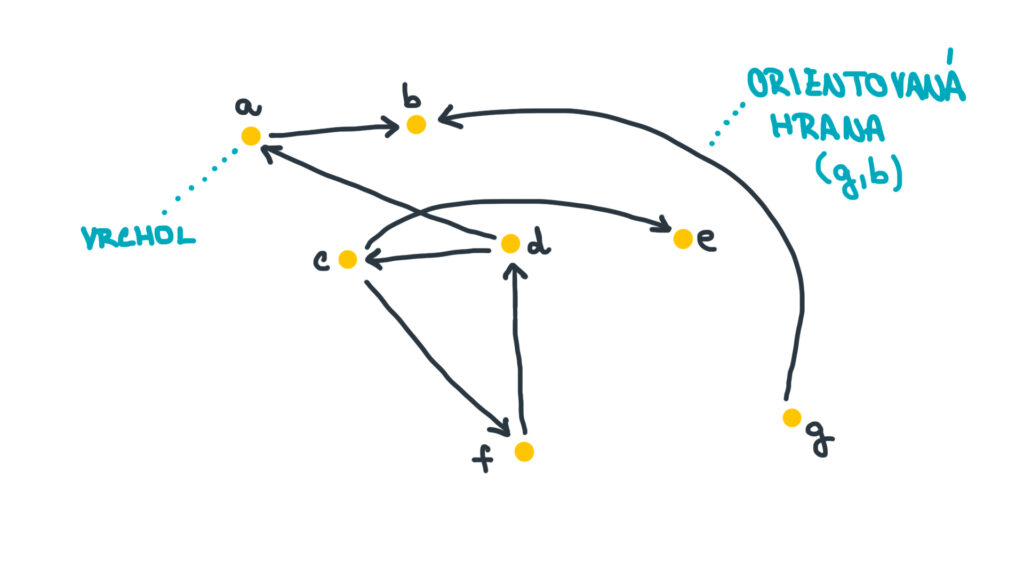
Obrázek opět asi řekne víc než tisíc definic od Elišky. Na obrázku 2 je obrázkově zakreslený příklad orientovaného grafu, který jsem pojmenovala \(G_2\) (aby se nám nepletl s grafem \(G_1\) výše). Matematicky bychom tento graf zapsali následovně: \(G_2 = (V_2, E_2)\), kde
- \(V_2 = \big\{ a,b,c,d,e,f,g \big\}\) a
- \(E_2 = \big\{ (a,b), (g,b), (c,e), (c,f), (f,d), (d,c), (d,a) \big\}\).
Zde je například vrchol \(g\) předchůdcem vrcholu \(b\).
Další pojem, který se může hodit, je stupeň vrcholu. Stupeň vrcholu v neorientovaném grafu je počet hran s ním propojených. Například na obrázku 1 výše má vrchol \(c\) stupeň 3. U orientovaného grafu můžeme ještě rozlišit vstupní stupeň vrcholu, tj. počet hran vedoucích do daného vrcholu, a výstupní stupeň vrcholu, tj. počet hran vedoucích z daného vrcholu. Například na obrázku 2 výše má vrchol \(c\) stupeň 3, výstupní stupeň 2 a vstupní stupeň 1.
V grafu se můžeme za pomoci hran mezi vrcholy pohybovat. Pokud budeme chtít mluvit o tom, že z nějakého vrcholu se můžeme po sledování několika navazujících hran za sebou dostat do jiného vrcholu, budeme používat pojem cesta. Cestou v grafu označujeme posloupnost navzájem různých vrcholů \(v_1, v_2, \dots, v_k\) takovou, že mezi každými dvěma vrcholy \(v_i, v_{i+1}\) jdoucími v posloupnosti po sobě, existuje hrana. Takovou cestu můžeme zkráceně nazvat \(v_1 – v_k\) cestou. V grafu může samozřejmě mezi dvěma vrcholy existovat více různých cest. Všimněte si ale, že z naší definice plyne, že žádné dva vrcholy (a tedy ani hrany) se v cestě neopakují. Délka cesty je potom počet hran, které cesta obsahuje (tj. číslo o jedna menší než je počet vrcholů, které jsou součástí cesty). Například na obrázku 1 výše existuje mezi vrcholy \(e\) a \(d\) jedna cesta délky 2 a jedna cesta délky 3 (a žádné jiné). Umíte je najít?
U orientovaného grafu můžeme vyžadovat respektování orientace hran a pak mluvíme o orientované cestě. Orientovaná cesta je tedy posloupnost vrcholů \(v_1, v_2, \dots, v_k\) taková, že existuje orientovaná hrana \((v_i, v_{i+1})\) pro všechny \(i \in \{ 1, \dots, k-1 \}\). Například na obrázku 2 výše existuje orientovaná cesta z vrcholu \(d\) do vrcholu \(b\) délky 2. Mezi vrcholy \(g\) a \(a\) existuje pouze cesta (tj. nebereme v úvahu orientaci), nikoliv ale orientovaná cesta.
Kromě cest můžeme v grafu najít někdy i cykly. Cyklus je zjednodušeně řečeno cesta, která začíná a končí ve stejném vrcholu (tj. povolíme opakování vrcholů, ale pouze u prvního a posledního). Opět platí, že u orientovaného grafu můžeme brát v potaz orientaci hran. Pak mluvíme o orientovaném cyklu. Například na obrázku 1 existuje cyklus mezi vrcholy \(c, d\) a \(f\) délky 3. Na obrázku 2 mezi těmito vrcholy existuje (i) orientovaný cyklus. Graf, který neobsahuje žádný cyklus, nazýváme acyklický. Pokud chceme vzít v potaz orientované cykly, pak existuje ještě pojem orientovaný acyklický graf, tím označujeme orientovaný graf bez orientovaných cyklů (ale „neorientované“ cykly — tj. cykly, kde nebere v potaz orientaci hran — takový graf obsahovat může).
Ještě jste tu? Paráda. To nejtěžší máme za sebou. Vážně. Nyní přichází na řadu další důležitá (ale jednodušší) nelineární datová strukturu a tou je strom.
Stromy 🌲 nerostou jen v přírodě
Strom je jednoduše řečeno graf, kterému trochu zastřihneme křidélka (nedovolíme mu všechny psí kousky jako třeba cykly). Přesněji definujeme strom jako neorientovaný graf, který je acyklický a souvislý. Souvislý neorientovaný graf je takový, kde mezi každými dvěma vrcholy existuje cesta. Třeba graf na obrázku 1 je souvislý, ale není acyklický, tedy to není strom. Pokud bychom mu ale umazali například hranu \(\{c, f\}\), pak už by to strom byl. (Mohli bychom smazat místo hrany \(\{c,f\}\) i jinou, aby vznikl strom?)
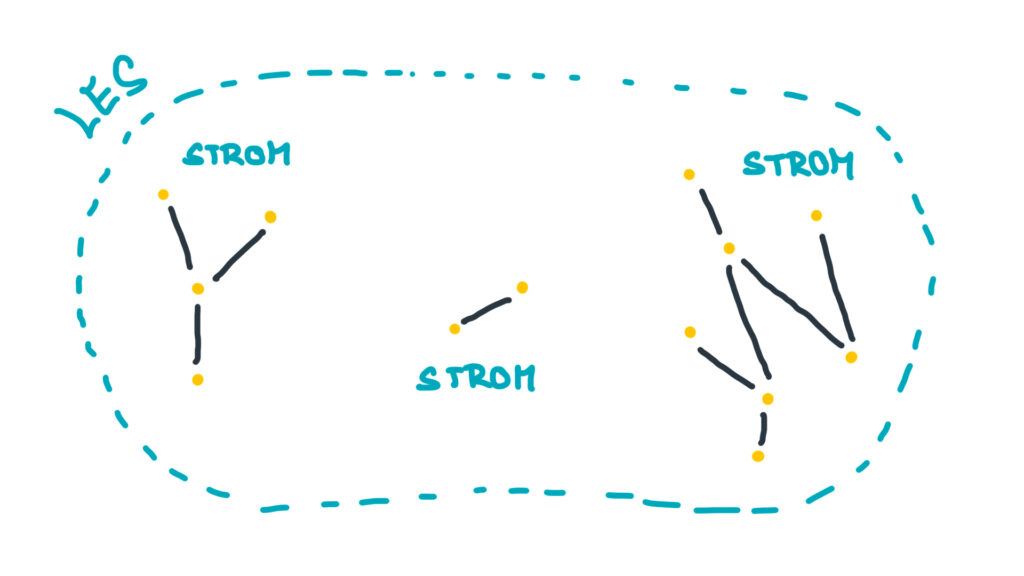
Když v definici souvislost vynecháme, tedy budeme chtít, aby byl neorientovaný graf pouze acyklický, dostaneme další pojem, a tím je les. Les je tedy neorientovaný acyklický graf. A víte co je krásné? Jednotlivé souvislé „shluky“ vrcholů v lese tvoří stromy. Takže les je tvořen stromy — přesně jako v přírodě. No, není to pěkný?
My se budeme přesněji bavit o zakořeněných stromech (a zakořeněném lese). Strom zakořeníme tím, že u něj vybereme jeden z vrcholů a prohlásíme jej za kořen. Protože u zakořeněných stromů existuje do všech vrcholů z kořene právě jedna cesta (fakt to tak je), můžeme vrcholy rozdělit do takzvaných hladin podle toho, v jaké vzdálenosti od kořene jsou. Čímž se dostávám k zakreslení zakořeněných stromů. V informatice je typicky zakreslujeme kořenem vzhůru (don’t judge us). Ostatní vrcholy potom pověsíme pod kořen a rozdělíme je do jim odpovídajících hladin. Zkuste si například „zakořenit“ jednotlivé stromy na obrázku 3.
Jakmile strom zakořeníme, vrcholy zaujmou vzájemný hierarchický vztah. Ten popisujeme rodinnými vztahy. Používáme pojmy jako rodič, dítě, sourozenci, předek a potomek. Pokud vrchol \(v\) leží na (jediné) cestě z kořene do vrcholu \(u\), pak \(v\) je předek vrcholu \(u\) a vrchol \(u\) je potomkem \(v\). Pokud jsou vrcholy \(u\) a \(v\) přímo propojeny hranou, tj. existuje hrana \(\{u,v\}\), pak \(u\) je rodičem vrcholu \(v\) a vrchol \(v\) je dítětem \(u\). Pokud dva vrcholy sdílejí stejného rodiče, nazýváme je sourozenci. Pokud vrchol nemá žádné děti, tak jej nazýváme listem. Vrcholy, které nejsou listy, nazýváme vnitřními vrcholy.
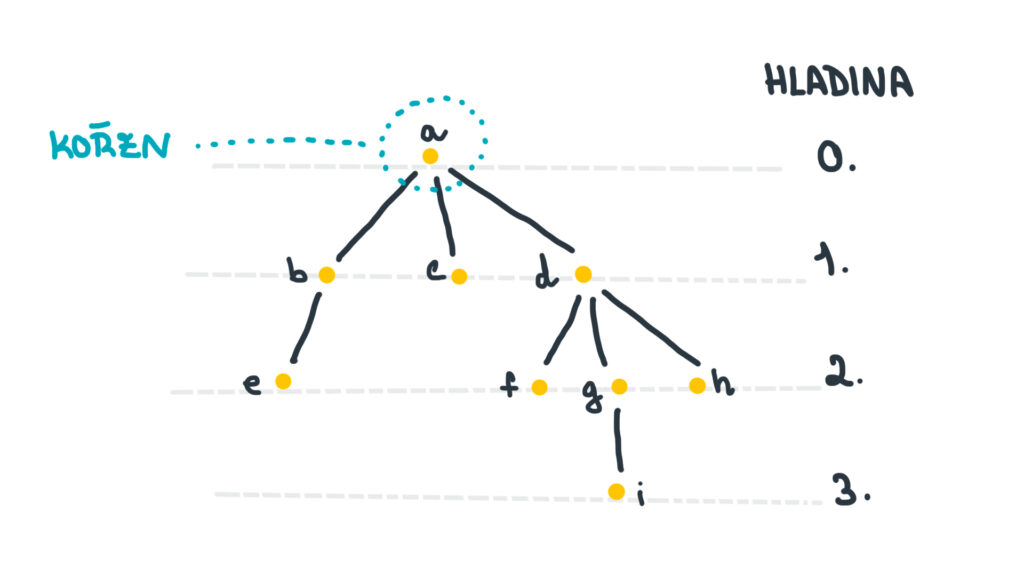
Pojďme si tyhle pojmy potrénovat na obrázku 4. Zde vrchol \(a\) je kořenem. Dále například vrchol \(d\) je rodičem vrcholů \(f, g\) a \(h\). Tyto vrcholy jsou tedy jeho děti. Vrcholy \(f, g\) a \(h\) jsou navzájem sourozenci, stejně jako třeba vrcholy \(b, c\) a \(d\). Vrchol \(d\) je předkem vrcholů \(f, g, h\) a \(i\). Tyto vrcholy jsou tedy jeho potomky. Vrchol \(a\) je předkem všech ostatních vrcholů. Vrcholy \(e, c, f, i\) a \(h\) jsou listy. Zbývající vrcholy jsou vnitřní.
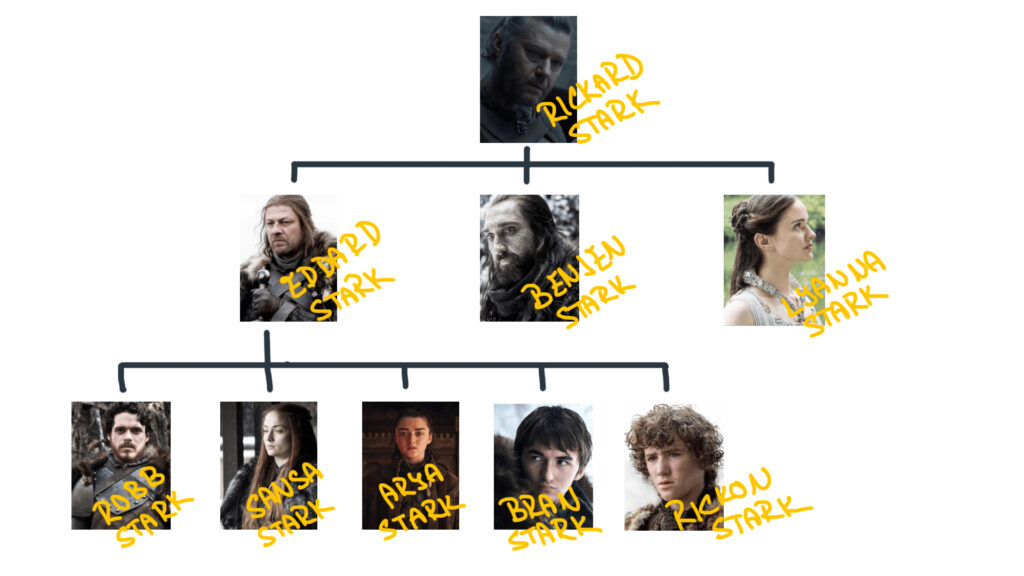
Tato terminologie vychází z rodinného stromu, což je grafické zobrazení rodokmenu. Konkrétně rodokmen můžeme (dle Wikipedie) zobrazit jako takzvaný vývod — začneme od daného člověka a jdeme po předcích nebo takzvaný rozrod — kdy kořenem stromu je daný člověk a postupně sledujeme linii jeho potomků. Terminologie, která se používá v informatice, vychází právě z té druhé varianty, rozrodu.
Vezměme si například kousek linie rodu Starků ze seriálu Hra o trůny. (Pokud jste tenhle seriál ještě neviděli, nebojte, nebudu spoilerovat, ale… teď vážně… vy jste neviděli Hru o trůny? Do you live under a rock?) Za kořen si zvolíme Rickarda Starka a vytvoříme pro něj rozrod. Získáme tak krásný zakořeněný strom. Vidíme, že Eddard Stark je rodičem 5 dětí (Robb, Sansa, Arya, Bran a Rickon). Ti jsou navzájem sourozenci. Rickard Stark je jejich prarodič, neboli předek.
Dalším příkladem stromové struktury v každodenním životě je uložení souborů v počítači. Zde máme kořenový adresář, pod ním můžeme mít další složky a nebo třeba soubory. Soubory jsou v tomto případě vždy listy (nemají potomky). Složky tvoří vnitřní vrcholy (a nebo i listy, pokud je daná složka prázdná).
Před naší, za naší, cesta 🛣 má ať nepráší
Jak jsme si už řekli, strom i graf jsou příklady nelineární datové struktury. Pro nelineární struktury je typické, že je nemůžeme „přečíst“ jedním průchodem (aniž bychom se nemuseli vracet). Při čtení se dostáváme do situací, kdy si musíme vybrat, kudy budeme pokračovat. Narážíme na křižovatky. Tím se nelineární datové struktury liší od lineárních. Hlavní charakteristikou lineární datové struktury je právě to, že k jejímu přečtení nám stačí jediný průchod. Je to jako bychom chtěli z města A dojet do města B a mezi nimi existovala pouze jedna silnice. Po cestě nás nečekají žádné křižovatky, u kterých bychom se museli rozhodovat, kterou cestou se vydat.
Pojďme si lineární datovou strukturu definovat přesněji. Lineární datová struktura (lineární seznam) je sekvence vrcholů \(v_1, v_2, \dots, v_k\), které jsou uspořádány v řadě za sebou. V lineárním seznamu je pro nás zajímavé pouze to, že \(v_1\) je počáteční vrchol, \(v_k\) je koncový vrchol a pro ostatní vrcholy \(v_i\), kde \(2 \leq i \leq k-1\) platí, že vrchol \(v_{i-1}\) je předchůdcem vrcholu \(v_i\) a vrchol \(v_{i+1}\) je následníkem vrcholu \(v_i\). Je to jako bychom navlékali korálky na nit, jeden korálek za druhým. Hmm. Nepřipomíná vám definice nelineární datové struktury něco? To jsou přece naše cesty v grafu ne?
Dámy a pánové, pojďme si to shrnout. Graf jsme si na začátku zavedli jako nejkomplexnější strukturu. U stromu jsme si řekli, že se jedná o zjednodušený graf. No a cesta je vlastně zjednodušený strom. Tedy každá cesta je zároveň stromem i grafem. A každý strom je zároveň grafem. Ale ne každý graf je stromem či cestou a ne každý strom je cestou. Graf v sobě ale „obsahuje“ cesty i stromy a strom v sobě obsahuje cesty. Makes sense?
Gratuluji! Právě jste se pochopili většinu látky probírané v prvních dvou týdnech semestru z předmětu Algoritmy a grafy 1, který učím spolu s kolegy u nás na fakultě ve druhém ročníku bakalářského studia.
Vy: „Aaaa k čemu nám to všechno bylo, Eliško?“
Já: „I hear you! Pojďme se společně podívat, jak tohle všechno souvisí se systémem zettelkasten.“
Matematická abstrakce 🤯 systému zettelkasten
Nebojte se, zní to obtížněji, než to ve skutečnosti bude (nezapomeňte, že vy už znáte spoustu pojmů z teorie grafů). Pojďme na to.
V naší matematické abstrakci budeme permanentní poznámky reprezentovat jako vrcholy. Propojení poznámek (vrcholů), pak budeme zakreslovat jako hrany. V sekci Luhmannův unikátní způsob propojování poznámek v tomto článku jsem vysvětlila, že Luhmann propojoval poznámky dvěma způsoby.
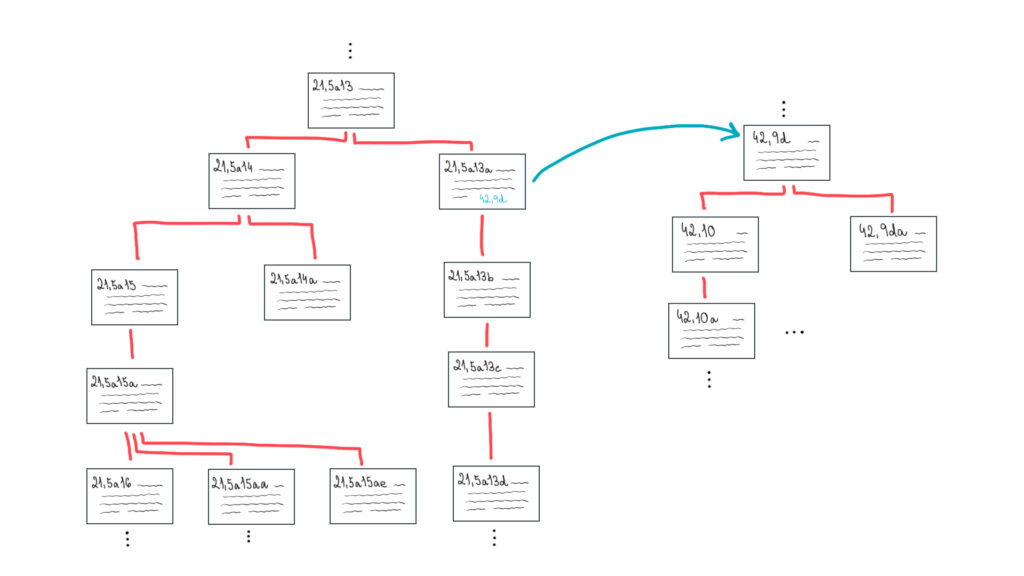
První propojení poznámek jsem nazvala implicitním. Toto propojení vychází z toho, jaký identifikátor má daná poznámka. Jedna poznámka v tomto případě jasně navazuje na předcházející. Jako v diskuzi. Implicitní propojení poznámek jsem na obrázku 2 vyznačila červeně. Pokud si na chvíli odmyslíte tu modrou hranu. Jakou datovou strukturu vám obrázek připomíná? Pokud říkáte strom, zakořeněný strom nebo dokonce zakořeněný les, tak se cítím jako pyšný rodič. Máte totiž pravdu. Červené hrany jsou vlastně stromové hrany. První poznámka započínající diskuzi je vždy kořenem stromu a protože diskuzí můžeme mít v systému zettelkasten obecně více, můžeme mít i více zakořeněných stromů. Zettelkasten je tedy zakořeněný les. Ale! To není všechno…
Druhý způsob propojení poznámek jsem nazvala křížovým. Tato propojení Luhmann používal, když potřeboval poznámku propojit s více poznámkami najednou. Na obrázku 2 jsem jedno takové křížové propojení vyznačila modrou orientovanou hranou. Protože poznámka 21,5a13a odkazuje na poznámku 42,9d, vede z ní orientovaná hrana právě do této poznámky. Pokud bychom si v Luhmannově systému zettelkasten odmysleli červené stromové hrany a ponechali tam pouze ty modré, dostali bychom orientovaný graf. Zettelkasten je tedy vlastně i orientovaný graf.
Pojďme se na to podívat ještě jinak. Představte si, že se systémem zettelkasten právě začínáte a chcete přidat svou první permanentní poznámku. Protože zettelkasten je prázdný, není nad čím přemýšlet. Poznámku tam vložíte. Tím jste vyrobili kořen nového zakořeněného stromu. Nyní si představte, že přidáváte druhou permanentní poznámku. Musíte se rozhodnout, jestli ji navážete na tu první, či nikoliv:
- Pokud ano, připojíte ji pod první poznámku jako dítě pomocí stromové hrany.
- Pokud se rozhodnete, že nová poznámka s tou první nesouvisí, prohlásíte ji za kořen dalšího zakořeněného stromu. V tom případě už náš zakořeněný les bude obsahovat dva zakořeněné stromy. Každý z nich o jednom vrcholu.
Postupně nám tedy takto porostou stromy (připojováním navazujících poznámek do již existujícího zakořeněného stromu) i les (pokud se poznámka nehodí, tak založíme nový zakořeněný strom). Každou novou poznámku, kterou připojujeme do již existujícího zakořeněného stromu, připojujeme jako dítě k některé již existující poznámce. Každá nově přidaná poznámka nemá žádné potomky a je tedy listem.
Kromě stromových hran zde ale máme ještě ty grafové, které reprezentují odkazy na další relevantní poznámky. Ty reprezentujeme pomocí orientovaných hran. Tyto hrany mohou z jednoho vrcholu vést v podstatě do libovolného dalšího v našem zakořeněném lese.
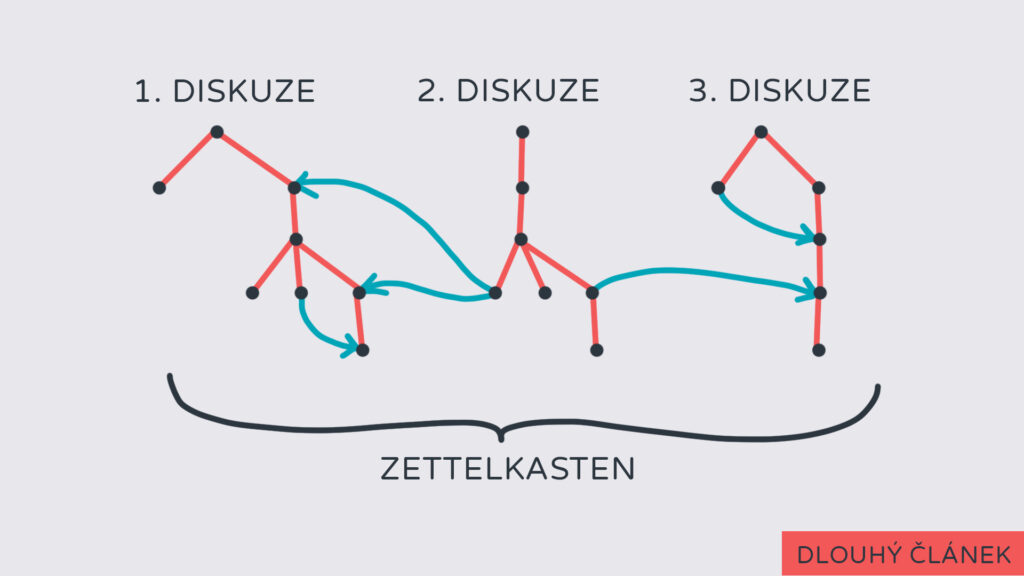
Takže sečteno a podtrženo, zettelkasten je kombinace dvou nelineárních datových struktur: zakořeněného lesa a orientovaného grafu. Pojďme vyvrcholit celou tuhle duševní matematickou pouť následující ilustrací:
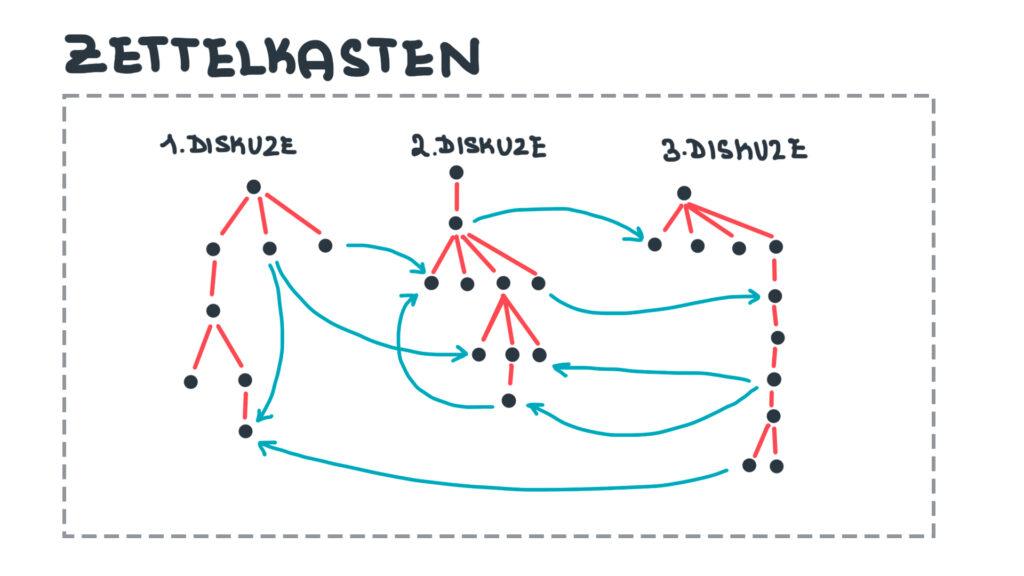
To je za teoretičku Elišku prozatím vše. Doufám, že se vám výlet do teorie grafů líbil. See you later.