Je součin dvou NEregulárních jazyků vždy NEregulární jazyk?

5.2. 2021 (Aktualizováno: 20.1. 2022)02077x

Určitě víte, že regulární jazyky jsou pro operaci součin (zřetězení) uzavřené. To znamená, že součin dvou libovolných regulárních jazyků je vždy opět regulární jazyk. Co se ale stane, když provedeme součin dvou NEregulárních jazyků? Bude výsledkem opět vždy neregulární jazyk? Nebo se může stát, že výsledný jazyk bude regulární? Nebo bude dokonce regulární vždy?

Na poslední otázku zvládneme odpovědět hned, neboť vymyslet protipříklad, ve kterém součin dvou neregulárních jazyků bude opět neregulární jazyk, je celkem trivka. Co třeba: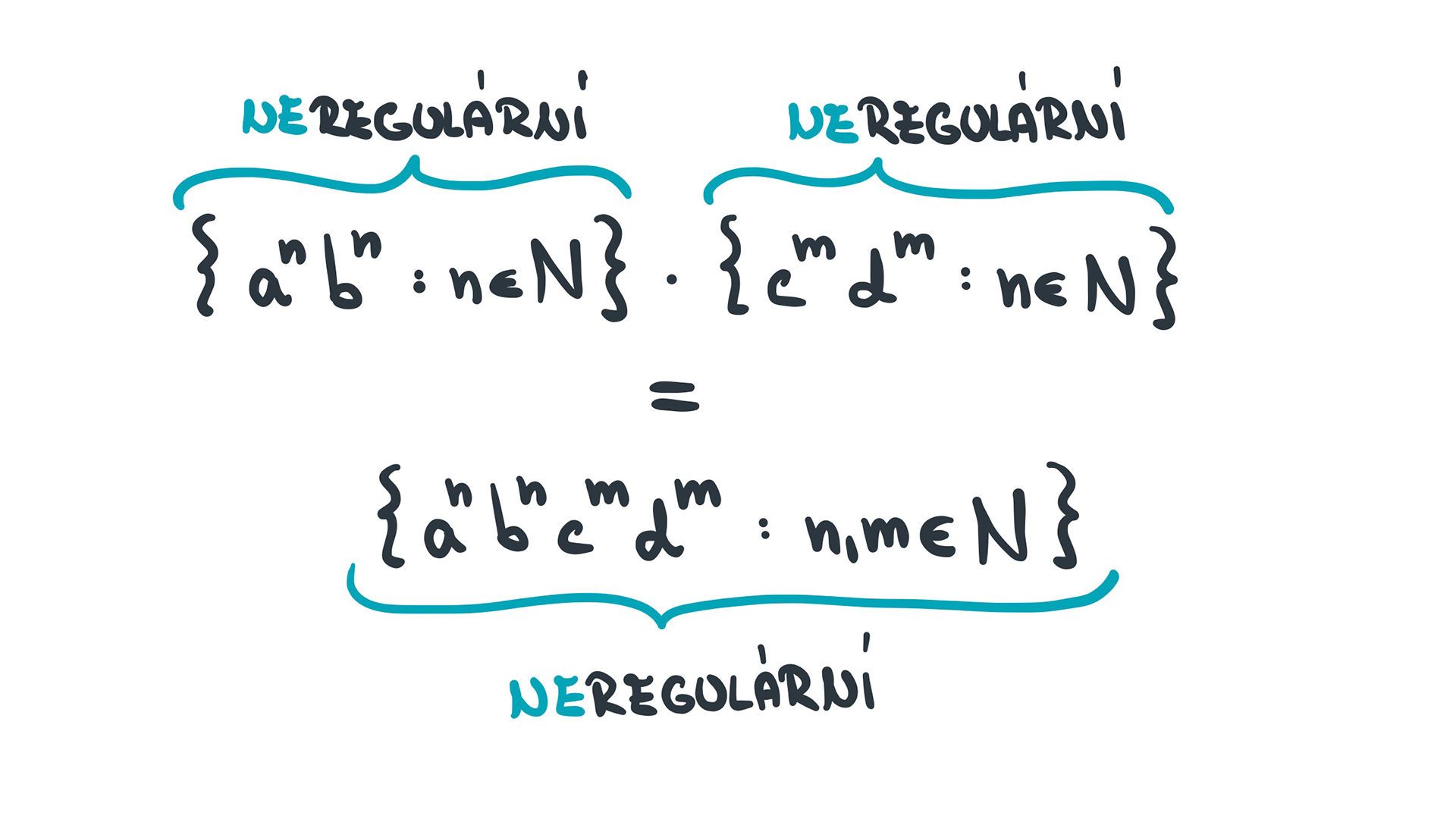(Důkazy, že tyto jazyky jsou opravdu neregulární, si jistě čtenář zvládne rozmyslet sám. Mrk. 😉)

Tím jsme si tedy dokázali, že součin dvou neregulárních jazyků může být jazyk neregulární. Musí to tak ale být vždy? Je součin dvou neregulárních jazyků vždy jazyk neregulární?

Pokus o důkaz tvrzení

Kdo dával ve škole pozor, určitě ví, že pro operaci součin jsou uzavřené nejen regulární jazyky, ale všechny třídy jazyků z Chomského hierarchie. Tedy výsledkem součinu dvou bezkontextových jazyků je vždy jazyk bezkontextový, výsledkem součinu dvou kontextových jazyků je vždy jazyk kontextový a výsledkem součinu dvou rekurzivně spočetných jazyků je vždy jazyk rekurzivně spočetný. Splňuje to i náš příklad:To je dobrý ne? Když tedy provedeme součin dvou neregulárních jazyků, které jsou například zrovna náhodou bezkontextové, pak výsledkem je vždy bezkontextový jazyk. Tedy výsledkem je neregulární jazyk. Nebo ne? Hmm. Pokud kroutíte hlavou, že se vám to nezdá, tak kroutíte správně.

Všechny regulární jazyky jsou totiž zároveň také bezkontextové, kontextové a rekurzivně spočetné. Pokud tedy provedeme součin dvou neregulárních jazyků, které jsou zrovna náhodou bezkontextové, pak výsledkem sice bude vždy bezkontextový jazyk. Tato vlastnost už nám ale nic neříká o tom, zdali náhodou není také regulární.

Fňuk. A tak nadějně to vypadalo! No nic, pojďme na to jinak. Dokázat tvrzení, že součin dvou neregulárních jazyků je vždy neregulární jazyk se nám nedaří. Tak co kdybychom ho zkusili vyvrátit? Jak na to? No stačí přece najít alespoň jeden protipříklad. Zkusíme najít dva neregulární jazyky, jejichž součinem získáme jazyk regulární.

Vyvrácení tvrzení (část první)

Hledáme tedy nějaké dva neregulární jazyky $L_1$ a $L_2$ takové, že $L_1 \cdot L_2$ je regulární jazyk. Vezměme si třeba následující dva jazyky nad abecedou $\{ \mathtt{a}, \mathtt{b} \}$:

$L_1 = \{ \mathtt{a}^i \mathtt{b}^j : i,j \in \mathbb{N}_0 \wedge i \neq j \},$
$L_2 = \{ \mathtt{b}^m \mathtt{a}^n : m,n \in \mathbb{N}_0 \wedge m \neq n \}.$

Tyto jazyky nejsou regulární. Důkaz v tomto případě ponechávám opět na čtenáři (use the Force, chci říct, pumping lemma). Anyway, tvrdím, že součinem těchto dvou jazyků získám jazyk regulární. Tedy

$$\underbrace{L_1}_{\text{neregulární}} \cdot \underbrace{L_2}_{\text{neregulární}} = \underbrace{\{ \mathtt{a}^i \mathtt{b}^{j+m} \mathtt{a}^n : i,j,m,n \in \mathbb{N}_0 \wedge i \neq j \wedge m \neq n\}}_{\text{regulární}}.$$

Asi bych se vás pro pořádek měla nejdřív zeptat, jestli mi vůbec věříte, že součin těchto jazyků vypadá takto. Do you? 🥺

\begin{nonbelievers}

Součin jazyků je přece definován tak, že

$$L_1 \cdot L_2 = \{ w : w = xy \wedge x \in L_1 \wedge y \in L_2 \}.$$

V součinu jsou tedy všechny možné řetězce, které vznikly zřetězením nějakého řetězce z jazyka $L_1$ s nějakým řetězcem z $L_2$. Řetězce z našeho $L_1$ vypadají tak, že jsou nejdříve symboly $\mathtt{a}$ a pak symboly $\mathtt{b}$, přičemž jich nesmí být stejný počet. Řetězce z našeho $L_2$ vypadají zase tak, že jsou nejdřív symboly $\mathtt{b}$ a pak symboly $\mathtt{a}$, přičemž jich nesmí být stejný počet. Když to dáme za sebe dostaneme:

$$\{\mathtt{a}^i \mathtt{b}^{j} \mathtt{b}^m \mathtt{a}^n : i,j,m,n \in \mathbb{N}_0 \wedge i \neq j \wedge m \neq n\}.$$

Což je ale přece to samé jako:

$$\{\mathtt{a}^i \mathtt{b}^{j+m} \mathtt{a}^n : i,j,m,n \in \mathbb{N}_0 \wedge i \neq j \wedge m \neq n\}.$$

\end{nonbelievers}

Vyvrácení tvrzení (část druhá bolestivá)

Ať má tenhle článek nějakou úroveň, nebudeme tady jen tak plácat rukama, ale formulujeme si následující roztomilé lemmátko.

Lemma: Jazyk $L = \{\mathtt{a}^i \mathtt{b}^{j+m} \mathtt{a}^n : i,j,m,n \in \mathbb{N}_0 \wedge i \neq j \wedge m \neq n\}$ je regulární.

Bystrý čtenář už ví, že pokud toto lemmátko nyní dokážeme, pak dostaneme odpověď na otázku, která je v názvu tohoto článku. Tak schválně, jaká že to bude odpověď?

Pokud jste už stihli zapomenout název tohoto článku, tak si jej prosím připomeňte. Abyste totiž v průběhu následující důkazu nepadli uprostřed bojiště, budete potřebovat spoustu motivace. Máte to? Tak nasadit přilby, kopí vpřed a jdeme na to.

Uvažujme pro začátek následujících pět jazyků:

$L_A = \{ \mathtt{b}^r : r \in \mathbb{N} \wedge r \geq 2 \}$,
$L_B = \{ \mathtt{b}^r \mathtt{a}^s : r,s \in \mathbb{N}\}$,
$L_C = \{ \mathtt{a}^r \mathtt{b}^s : r,s \in \mathbb{N} \}$,
$L_D = \{ \mathtt{ab}^r \mathtt{a} : r \in \mathbb{N}_0 \wedge r \neq 1 \}$,
$L_E = \{ \mathtt{a}^r \mathtt{b}^s \mathtt{a}^t : r,s,t \in \mathbb{N}_0 \wedge r,t \geq 1 \wedge (r \neq 1 \vee t \neq 1) \}$.

K čemu nám tyto jazyky budou? Chvilka napětí… Sjednocením těchto pěti jazyků totiž dostaneme právě jazyk $L$. Huh? Tady se asi budete muset chvilku zastavit a rozmyslet si to (čtěte: napsat si to). Chceme vlastně dokázat následující rovnost: $$L = L_A \cup L_B \cup L_C \cup L_D \cup L_E.$$

To uděláme tak, že dokážeme následující dvě inkluze:

$L_A \cup L_B \cup L_C \cup L_D \cup L_E \subseteq L,$
$L \subseteq L_A \cup L_B \cup L_C \cup L_D \cup L_E.$

Není těžké si rozmyslet, že každý z pěti výše uvedených jazyků je podmnožinou jazyka $L$. První inkluzi vám tedy ponechám jako cvičení. Podíváme se spolu na tu druhou. Neobsahuje totiž jazyk $L$ něco navíc?

Přemýšlejte nad tím následovně: Je-li $w \in L$, pak je z definice jazyka $L$ ve tvaru $w = \mathtt{a}^i\mathtt{b}^{j+m}\mathtt{a}^n$, kde $i,j,m,n \in \mathbb{N}_0$ a zároveň $i \neq j$ a $m \neq n$. Podle hodnot exponentů $i,j,m,n$ můžeme potom rozlišit následujících pět případů:

Případ, kdy $i = 0 \wedge n = 0$. Tož pak přece musí platit, že $j \neq 0 \wedge m \neq 0$, tedy $j,m \geq 1$. Takové řetězce patří do jazyka $L_A$.
Případ, kdy $i = 0 \wedge n \neq 0$. Pak musí platit, že $j \neq 0$. Tedy $j,n \geq 1$. Takové řetězce patří do jazyka $L_B$.
Případ, kdy $i \neq 0 \wedge n = 0$. Pak musí platit, že $m \neq 0$. Tedy $i,m \geq 1$. Takové řetězce patří do jazyka $L_C$.
Případ, kdy $i,n = 1$. Pak nutně $j+m \neq 1$. A takové řetězce patří do jazyka $L_D$.
Ostatní případy, tj. zbylé hodnoty exponentů, které nevyhovují žádné z předchozích podmínek. Takové řetězce patří do jazyka $L_E$.

Uff. Tím jsme dokázali, že $L$ je podmnožinou sjednocení našich pěti jazyků. A druhou inkluzi jste si rozmysleli na začátku (rozmysleli, že ano?). Dohromady tedy máme ověřeno, že $$L = L_A \cup L_B \cup L_C \cup L_D \cup L_E.$$

Ještě žijete? Otřete krev a pot, nadechněte se a pokračujeme! Už jsme u nepřátelských hradeb! Pojďme si ukázat, že každý z našich pěti jazyků ve sjednocení je regulární. (Wait, what?)

Jazyk $L_A = \{ \mathtt{b}^r : r \in \mathbb{N} \wedge r \geq 2 \}$ je regulární. Snadno ověříme, že jej lze popsat například regulárním výrazem $\mathtt{bb}\mathtt{b}^*$.

Jazyk $L_B = \{ \mathtt{b}^r \mathtt{a}^s : r,s \in \mathbb{N}\}$ je regulární. Snadno ověříme, že jej lze popsat například regulárním výrazem $\mathtt{bb}^*\mathtt{aa}^*$.

Jazyk $L_C = \{ \mathtt{a}^r \mathtt{b}^s : r,s \in \mathbb{N} \}$ je regulární. Snadno ověříme, že jej lze popsat například regulárním výrazem $\mathtt{aa}^*\mathtt{bb}^*$.

Jazyk $L_D = \{ \mathtt{ab}^r \mathtt{a} : r \in \mathbb{N}_0 \wedge$ $r \neq 1 \}$ je regulární. Snadno ověříme, že jej lze popsat například regulárním výrazem $\mathtt{a}\mathtt{a} + \mathtt{a}\mathtt{bbb}^*\mathtt{a}$.

Jazyk $L_E = \{ \mathtt{a}^r \mathtt{b}^s \mathtt{a}^t : r,s,t \in \mathbb{N}_0 \wedge$ $r,t \geq 1 \wedge$ $ (r \neq 1 \vee t \neq 1) \}$ je regulární. Tady už to možná není tak očividné. Pojďme se tu na chvíli zastavit a rozmyslet si dva případy:

Pokud $s = 0$, dostáváme $\{ \mathtt{a}^{r+t} : r,t \in \mathbb{N} \, \wedge $ $(r \neq 1 \vee t \neq 1)\}$ a tuto část lze očividně popsat regulárním výrazem $V_1 = \mathtt{aaaa}^*$.
Pokud $s \geq 1$ (Stay with me! Almost there!), dostáváme $\{ \mathtt{a}^r \mathtt{b}^s \mathtt{a}^t : r,s,t \in \mathbb{N} \, \wedge$ $(r \neq 1 \vee t \neq 1) \}$ a tuto část lze (možná méně očividně) popsat regulárním výrazem

$$V_2 = \underbrace{\mathtt{abb}^*\mathtt{aaa^*}}_{r=1 \wedge t \geq 2} + \underbrace{\mathtt{aaa}^*\mathtt{bb}^*\mathtt{a}}_{t=1 \wedge r \geq 2} + \underbrace{\mathtt{aaa}^*\mathtt{bb}^*\mathtt{aaa}^*}_{r,t \geq 2}.$$

Jazyk $L_E$ lze tedy popsat regulárním výrazem $V_1 + V_2$.

Uff. Proč, že jsme to vlastně dělali? Jasně, protože $L = L_A \cup L_B \cup L_C \cup L_D \cup L_E$. A když teď už víme, že $L_A, L_B, L_C, L_D$ i $L_E$ jsou regulární jazyky, tak i víme, že $L$ je regulární jazyk, neboť regulární jazyky jsou uzavřené pro operaci sjednocení. Pohoda ne? No dobře. Souhlasím, že to bylo trochu dlouhé a výpočetně bolestivé. Ale vaše vědomosti jsou zase o něco bohatší.

Závěr? Výsledkem součinu dvou neregulárních jazyků nemusí být vždy jazyk neregulární.(Disclaimer: Tento článek nenabádá čtenáře ke konzumaci alkoholu. Nápoj ve skleniččce na obrázku je jahodový džus.)

Komentáře

Je součin dvou NEregulárních jazyků vždy NEregulární jazyk?

Pokus o důkaz tvrzení

Vyvrácení tvrzení (část první)

Vyvrácení tvrzení (část druhá bolestivá)

Přidat komentář Zrušit odpověď